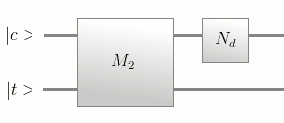
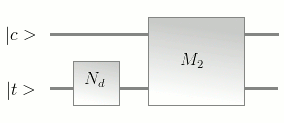Being similar to the DFT matrix, QFT matrix

has all the properties of DFT matrix.
Some properties are listed below
1)  , means
, means 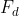 is unitary matrix , like every other Quantum Operator.
is unitary matrix , like every other Quantum Operator.
2) 
3)  So
So 
Now we focus on the powers of

.
We have
When m+n = 0(mod d)we have

on other cases the summation is is zero.So we have the
let

So we have .
Now
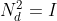
(this is easy to prove). then
So we have the following results.
Note that
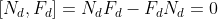
so they commute.
Now let us consider a qudit system with d- cannonical states
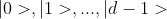
, Consider the quantum Operator
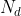
acting on any canonical state
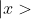
, we have
Consider the ring of integers
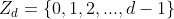
with normal addition and multiplication being the ring operations. Then we can view the operator
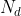
as
where
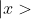
is a canonical state, where negation is the group negation operation. This is equivalent to time reversal in the DFT case.
Simplest
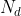
matrices are given below.